GPS定位笔记1(三边测量及多边测量，DOP)

杰罗姆

GPS定位笔记1(三边测量及多边测量，DOP)
杨熙

胡同里的技术土著。 善良， 专注

本文介绍三边测距及多边测距原理及实例。

牛顿迭代

见 https://zhuanlan.zhihu.com/p/56598915

名词术语

• multilateration: 多边测距
• trilateration: 三边测距
• presudo range： 伪距(一般通过传感器测量得到)
  

三边及多边测距

用户通过测量三个发射机(基站，或者卫星)的距离来定位自己的位置。最少三个发射机就可以计算用户位置(三边测距)，更多的发射机可以使用最小二层方法计算用户位置的最优解(多边测距)

三边测距

计算方法：

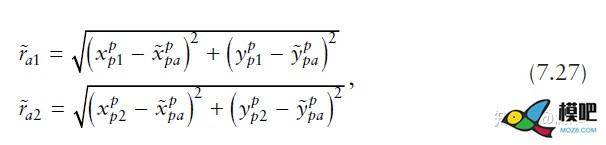
其中：发射机的位置为 <span class="MathJax_SVG" id="MathJax-Element-4-Frame" tabindex="0" data-mathml="(xp1p,yp1p)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">(xp1p,yp1p) 和 <span class="MathJax_SVG" id="MathJax-Element-1-Frame" tabindex="0" data-mathml="(xp2p,yp2p)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">(xp2p,yp2p) ，用户设备测得的到发射机的位置为 <span class="MathJax_SVG" id="MathJax-Element-5-Frame" tabindex="0" data-mathml="r~a1" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">r~a1 和 <span class="MathJax_SVG" id="MathJax-Element-6-Frame" tabindex="0" data-mathml="r~a2" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">r~a2 .计算得到的用户位置为： <span class="MathJax_SVG" id="MathJax-Element-2-Frame" tabindex="0" data-mathml="(x~pap,y~pap)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">(x~pap,y~pap) 。

一般的解法为，先给一个初始的用户位置的初值(预测值)： <span class="MathJax_SVG" id="MathJax-Element-3-Frame" tabindex="0" data-mathml="(x^pap−,y^pap−)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">(x^pap−,y^pap−) ，如7.28所示：

对7.28进行一阶泰勒展开得到：

其中H矩阵是7.27对用户距离的偏导数，H矩阵叫做量测矩阵或者几何矩阵：

多边定位例子

已知发射机和用户位置如下：通过三边定位法计算用户距离

已知三个接收机坐标和用户真实坐标(实际中应该是未知的)，和预测的用户坐标

首先计算预测的用户坐标与各个发射机之间的距离：

计算几何矩阵：
套公式并计算第一次迭代结果

之后进行第二次，第三次迭代计算即可，最终得到计算出来的用户位置：

三次迭代后的结果，用给出的用户真实位置相当接近

对应matlab代码：

%% 最小二乘法多边测距% pos, 上一次预测的用户位置% sv_pos: 发射机(基站，卫星)的坐标% pr: 传感器测量得到的伪距function pos = ch_multilateration(pos, sv_pos,  pr)%% 方法1：http://home.ustc.edu.cn/~huang83/wsn/localization.pdf% pr = pr(1:size(sv_pos, 2));%% b = vecnorm(sv_pos).^(2) - pr.^(2);% b = b(1:end-1) - b(end);% b = b';%% A =  sv_pos - sv_pos(:,end);% A = A(:,1:end-1)'*2;%% p = (A'*A)^(-1)*A'*b;%% 方法2%卫星个数n = size(sv_pos, 2);if n < 3    returnendB1=1;END_LOOP=100;while (END_LOOP > B1)        % 获得当前位置与各个基站的距离    r = vecnorm(sv_pos - pos);        % 求得H矩阵    H = (sv_pos - pos) ./ r;    H =-H';        %距离差值    dp = (pr - r)';    delta =  (H'*H)^(-1)*H'*dp;    END_LOOP = vnorm(delta);    pos = pos + delta;endend

调用

clear;clc;close all;addpath('../../library/nav_lib'); %% INPUTS: INITIAL CONDITIONpos_user_true = [1000, 100]';pos_user_inital = [0, 0]';pos_user = pos_user_inital;anchor_pos  = [0,1000; 0 -1000; 2000, 100]';pr = vecnorm(anchor_pos - pos_user_true);    pos_user = ch_multilateration(pos_user, anchor_pos, pr);

最终得到结果：

pos_user =          1000.00000137914          99.9999989638578
卫星伪距定位

与上面的算法类似，卫星的伪距定位可以看做一个加强版的多边定位算法。伪距一般记做 <span class="MathJax_SVG" id="MathJax-Element-7-Frame" tabindex="0" data-mathml="ρ" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">ρ ，一般通过发送和接收之间的时间差再乘以光速获得。但是由于发送和接收端的时钟有钟差，无线电在空中传播也有各种误差。所以伪距一般与真实距离有很大误差，这也是叫做伪距原因。记住，伪距是一个测量值！

对于GNSS系统， <span class="MathJax_SVG" id="MathJax-Element-8-Frame" tabindex="0" data-mathml="r(n)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">r(n) 是接收机到卫星n的几何距离，既：

[img=602,40][/img]" data-size="normal" data-rawwidth="602" data-rawheight="40" class="origin_image zh-lightbox-thumb lazy" width="602" data-original="https://pic1.zhimg.com/v2-2130776d37baee2bbc9ae35a8fa4338c_r.jpg" data-actualsrc="https://pic1.zhimg.com/v2-2130776d37baee2bbc9ae35a8fa4338c_b.png" style="display: block; margin-right: auto; margin-left: auto; max-width: 100%; height: auto; cursor: zoom-in;">
欧式空间距离公式

其中 <span class="MathJax_SVG" id="MathJax-Element-9-Frame" tabindex="0" data-mathml="x=[x,y,z]⊤" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">x=[x,y,z]⊤ 是未知接收机的位置坐标向量， <span class="MathJax_SVG" id="MathJax-Element-10-Frame" tabindex="0" data-mathml="x(n)=[x(n),y(n),z(n)]T" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">x(n)=[x(n),y(n),z(n)]T 是卫星n的位置坐标向量。那么定位算法的本质相当于求解四元非线性方程组：

通俗的讲，GPS定位的基本原理是三角学，即通过测量接收机到多颗卫星的距离，再根据简单的三角关系来推算接收机自身的位置。俗称伪距定位。

伪距定位算法

采用牛顿迭代进行求解，讲非线性方程线性化，以方程5.31中第n个方程式为例，对距离r 对x求偏导，得到

线性化，求偏导

其中 <span class="MathJax_SVG" id="MathJax-Element-12-Frame" tabindex="0" data-mathml="r(n)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">r(n) 是卫星n在用户接收机处得到的观测矢量长度（伪距）， <span class="MathJax_SVG" id="MathJax-Element-11-Frame" tabindex="0" data-mathml="(x(n)−x)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">(x(n)−x) 是此观测矢量的X分量，于是 <span class="MathJax_SVG" id="MathJax-Element-14-Frame" tabindex="0" data-mathml="x(n)−xr(n)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">x(n)−xr(n) 就等于单位观测矢量 <span class="MathJax_SVG" id="MathJax-Element-13-Frame" tabindex="0" data-mathml="I(n)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">I(n) 的X分量 <span class="MathJax_SVG" id="MathJax-Element-15-Frame" tabindex="0" data-mathml="Ix(n)" role="presentation" style="display: inline-block; line-height: normal; font-size: 16px; word-spacing: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">Ix(n) ，既

这个公式的Xn -X应该是写错了，应该是Rn-R

类似的，对XYZ都这么干，可以得到：

可以简化为：

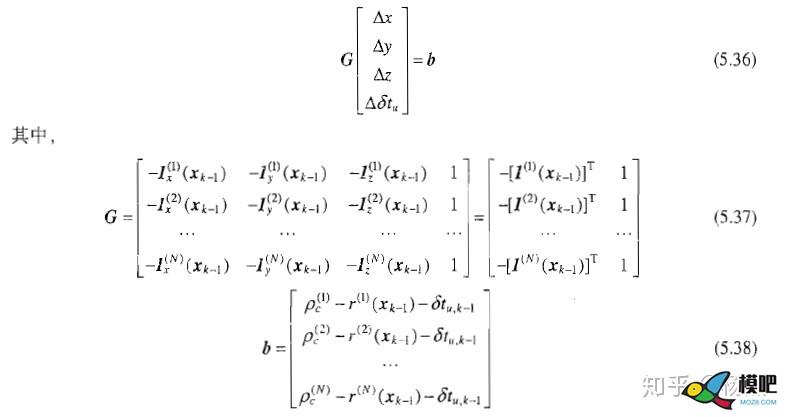
最后求解即可以用最小二乘法：

最后进行牛顿迭代，直到收敛即可：

另一种多边测距方法：
卫星伪距定位例子

假设有输入如下，给出用户真实坐标，当前估计坐标，估计钟差和 各个卫星位置

用牛顿迭代+最小二乘法计算用户坐标：

首先计算伪距：

这里是仿真，所以用真实坐标来计算的，再实际应用中，伪距是车辆量，是通过时间乘以光速来获得的。

第一次迭代： 计算各个卫星与估计位置的距离

计算几何矩阵：

迭代一次，得出结果：
第一次迭代后的结果：

对应的matlab代码：

最小二乘法计算位置函数：

% GPS 伪距最小二乘法求解， 状态量为 X Y Z B(钟差)function x = ch_gpsls(x, sv_pos,  pr)B1=1;END_LOOP=100;%卫星个数n = size(sv_pos, 2);while (END_LOOP > B1)    % 获得当前位置与各个基站的距离    r = vecnorm(sv_pos - x(1:3));        % 求得H矩阵    H = (sv_pos - x(1:3)) ./ r;    H =-H';        H = [H(:,1:3),  ones(n,1)];        b = ((pr - r) - x(4))';        % 迭代用户距离    delta =  (H'*H)^(-1)*H'*b;    x = x + delta;        END_LOOP = vnorm(delta(1:3));end%End of Whileend

例子：

clear;clcclose all;%% inital statetrue_user_states = [4245849 -2451342 4113840, 1000000]';station = zeros(3,5);station(:,1) = [21630742.37 -7872946.37 13290000]';station(:,2) = [9799722.428 -11678854.4 21773061.34]';station(:,3) = [15014045.82 2647381.37 21773061.34]';station(:,4) = [17020279.96 -20283979.8 2316599.642]';station(:,5) = [26076581.77 4598004.93 2316599.642]';x = zeros(4,1);%% presduo rangepr = vecnorm(station - true_user_states(1:3)) + true_user_states(4) ;x = ch_gpsls(x, station,  pr);

最终结果：

定位例子最终结果
参考

• 谢刚：GPS原理及接收机设计
• GNSS与惯性及多传感器组合导航系统原理-第二版.pdf 随书光盘Example9.1
• http://home.ustc.edu.cn/~huang