马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有帐号?立即注册

x
本帖最后由 duan123 于 2013-12-3 18:51 编辑
本文作者mmcopter,原地址:http://www.amobbs.com/thread-5483278-1-1.html
又花了将近一个星期,终于把姿态解算的框架完成了。仅仅是把陀螺仪、加速度计、罗盘融合在一起,得出旋转姿态,没有对加速度积分,没有用到气压计,几乎没有滤波。算是阶段性的工作吧,把框架设计得合理一点,以后添加/修改就很简单了。
从传感器的读取,到四元数的学习,到空间旋转的处理方法,循序渐进,逐个击破。主要参考了以下资料(按阅读的时间循序):
下面总结一下“姿态解算”的过程,分为“传感器”、“四元数与旋转”、“姿态解算框架”、“长期融合”、“快速融合”四部分。 - 传感器
我用的是10轴姿态传感器模块,其中陀螺仪是L3G4200D,加速度计是ADXL345,罗盘是HMC5883L,气压计是BMP085。全部都通过一条共用的I2C总线访问,速度都支持400kHz。
先讲讲I2C库。要配置、读取传感器,首先把通信做好,这里就是I2C库了。现在大部分单片机都有支持中断的硬件I2C了,可以写个高效的I2C库。我只实现了主机发送和主机接收模式,这里简单介绍一下接口。接口函数主要有2个:
- uint8_t I2C_transmit (uint8_t which,I2C_transmitCallback cb);
- void I2C_setNextCallback (uint8_t which,I2C_transmitCallback cb);
复制代码
I2C_transmit()用于触发一次传输(发送或接收),异步执行,调用后马上返回。其中有一个I2C_transmitCallback类型的参数,就是决定发送或接收、如何处理数据的回调函数了,其定义如下:- /*
- * 数据传输回调函数。
- * 每(准备)传输一个字节都调用一次。
- * 参数:
- * seq => 序号,第一次调用时为0,以后每次调用递增。
- * data => seq==0时写(从机地址+W/R)到data。
- * seq!=0时data是数据。发送就写data,接收就读data。
- * 返回值表示下一步的行为:
- * I2C_RT_START => 发送开始信号。
- * I2C_RT_STOP => 发送停止信号。
- * I2C_RT_REPEAT_START_OR_STOP => 如果有下一次传输,就发送RepeatStart,否则发送Stop。
- * I2C_RT_ACK => 继续传送,回应ACK。
- * I2C_RT_NACK => 继续传送,回应NACK。 */
- typedef uint8_t (* I2C_transmitCallback)(uint8_t seq,uint8_t * data);
复制代码
当用I2C_transmit()成功触发一次传输后,I2C库会根据需要调用回调函数,所以使用这个I2C库就是写回调函数了。而I2C_setNextCallback()则是用来设置紧接着的一次传输的。当本次传输结束时,不发送“Stop”信号,而是发送“RepeatStart”信号,然后开始下一个传输。利用这个函数可以发起连续多次传输。
有了I2C库就可以操作传感器了,以L3G4200D为例讲解。先看看DataSheet,操作L3G4200D有两个步骤,首先配置好寄存器,然后不断获取数据。配置寄存器比较简单,就是发送一段数据,用到两个函数:- /*
- * 初始化芯片。
- * 返回值 : {L3G4200D_RT_NORMAL,L3G4200D_RT_BUS_BUSY} */
- uint8_t l3g4200d_init(void)
- {
- if(I2C_transmit(L3G4200D_WHICH_I2C,l3g4200d_init_callback) == I2C_RT_TRANSMIT_NORMAL)
- return L3G4200D_RT_NORMAL;
- return L3G4200D_RT_BUS_BUSY;
- }
- /*
- * 初始化使用的I2C回调函数。 */
- uint8_t l3g4200d_init_callback(uint8_t seq,uint8_t * data)
- {
- const static uint8_t value[] = {
- I2C_addressToByte_write(L3G4200D_ADDRESS), /* 总线地址。 */
- (0x80 | 0x20), /* 寄存器地址。或0x80表示连续写。*/
- 0xEF, /* CTRL_REG1 */
- 0x00, /* CTRL_REG2 */
- 0x00, /* CTRL_REG3 */
- 0x00, /* CTRL_REG4,250dps量程。 */
- /* 其它默认。 */
- };
- //
- if(seq == sizeof(value))
- return I2C_RT_STOP;
- //
- *data = value[seq];
- return I2C_RT_ACK;
- }
复制代码
读取数据就有点麻烦,因为读之前要设置寄存器指针,所以其实包含两次传输:第一次是发送,设置当前寄存器指针;第二次是接收,获取测量值。第一次传输结束前要用I2C_setNextCallback()设置第二次传输的回调函数。见代码:- /*
- * 获取角速度。
- * 异步,读取成功后,l3g4200d_measureCompleted()会被调用。
- * 返回值 : {L3G4200D_RT_NORMAL,L3G4200D_RT_BUS_BUSY} */
- uint8_t l3g4200d_measureOmega(void)
- {
- if(I2C_transmit(L3G4200D_WHICH_I2C,l3g4200d_measureOmega_callback_reg) == I2C_RT_TRANSMIT_NORMAL)
- return L3G4200D_RT_NORMAL;
- return L3G4200D_RT_BUS_BUSY;
- }
- /*
- * 读角速度的I2C回调函数,设置当前寄存器地址。 */
- uint8_t l3g4200d_measureOmega_callback_reg(uint8_t seq,uint8_t * data)
- {
- if(seq == 0)
- {
- *data = I2C_addressToByte_write(L3G4200D_ADDRESS);
- return I2C_RT_ACK;
- }
- if(seq == 1)
- {
- *data = L3G4200D_REG_OMEGA; /* 角速度数据的寄存器地址。 */
- return I2C_RT_ACK;
- }
- //
- I2C_setNextCallback(L3G4200D_WHICH_I2C,l3g4200d_measureOmega_callback_read);
- return I2C_RT_REPEAT_START_OR_STOP;
- }
- /*
- * 读角速度的I2C回调函数,读取数据。 */
- uint8_t l3g4200d_measureOmega_callback_read(uint8_t seq,uint8_t * data)
- {
- if(seq == 0)
- {
- *data = I2C_addressToByte_read(L3G4200D_ADDRESS);
- return I2C_RT_ACK;
- }
- if(seq > L3G4200D_BUFFER_SIZE)
- return I2C_RT_STOP;
- //
- l3g4200d_var.buffer_8u[seq-1] = *data;
- if(seq == L3G4200D_BUFFER_SIZE)
- {
- l3g4200d_measureCompleted();
- return I2C_RT_NACK;
- }
- return I2C_RT_ACK;
- }
复制代码
这样就可以读取角速度了。所有数据都是在I2C中断里处理,所以要注意数据安全性,合理利用volatile。
其他传感器的工作方式几乎一样,Crtl+C,Ctrl+V,然后改改名字,改改参数就可以用了。 - 四元数与旋转
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量,欧拉角最直观,轴角表示则适合几何推导,而在组合旋转方面,四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存组合姿态、辅以矩阵来变换向量的方案。下面介绍一下四元数,然后给出几种旋转表示的转换。
四元数可以理解为一个实数和一个向量的组合,也可以理解为四维的向量。这里用一个圈表示q是一个四元数,很可能不是规范的表示方式。
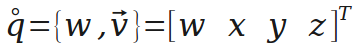
四元数的长度(模)与普通向量相似。
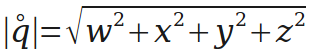
下面是对四元数的单位化,单位化的四元数可以表示一个旋转。
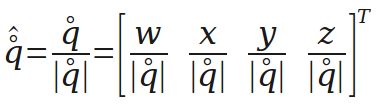
四元数相乘,旋转的组合就靠它了。
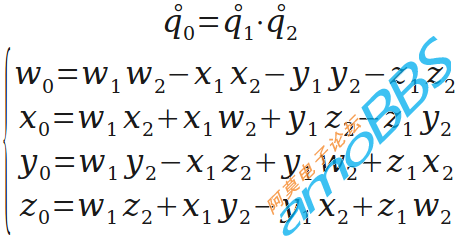
旋转的“轴角表示”转“四元数表示”。这里创造一个运算q(w,θ),用于把绕单位向量w转θ角的旋转表示为四元数。
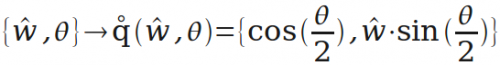
通过q(w,θ),引伸出一个更方便的运算q(f,t)。有时需要把向量f的方向转到向量t的方向,这个运算就是生成表示对应旋转的四元数的。后面会用到。
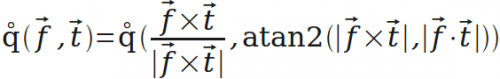
然后是“四元数表示”转“矩阵表示”。再次创造运算,用R(p)表示四元数p对应的矩阵(后面用到)。
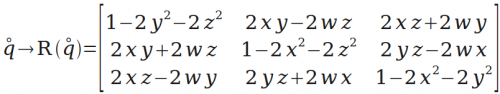
多个旋转的组合可以用四元数的乘法来实现。
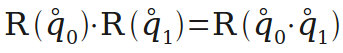
“四元数表示”转“欧拉角表示”。
 - 姿态解算框架
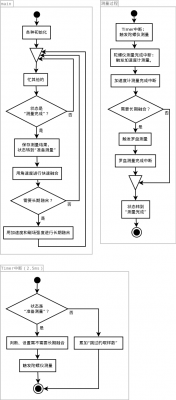
姿态解算框架其实就是程序框架了。设计框架既要准确,又要高效。总体设计是这样的:
- 用一个计时器定时触发测量;
- 所有测量过程都靠中断推进;
- 在main函数里不断检查测量是否完成,完成就进行解算。
测量过程比较耗时间,而这样设计,测量和解算可以同时进行,不会浪费CPU时间在(等待)测量上。而通过计时器触发测量,最大限度保证积分间隔的准确。
 - 长期融合
长期融合的目的有两个:一、得到初始姿态;二、用直接测量的姿态(下称直接姿态),纠正陀螺仪积分得出的姿态。直接测量的量包括加速度和磁场强度。长期融合有两个阶段,第一阶段是获得直接姿态,第二阶段是用直接姿态纠正当前姿态。首先讲第一阶段:用加速度和磁场强度计算直接姿态。
获取直接姿态的过程,其实是利用了空间中的两个场——重力场和地磁场,把测得的加速度和磁场强度旋转到“原来的位置”,其中的“旋转”就是我们需要的直接姿态了。但由于干扰和误差,测得的值不可能旋转到与实际的场一致。
用了净两天的时间来思考,还是想不出高效的办法。下面讲我的笨办法。
首先定义几个量("w" for world,"m" for measure):

单位化:
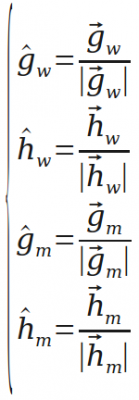
变换到对角线和平面法线。因为不能把加速度和磁场强度旋转到与对应的场一致,于是变换一下,使他们的对角线和平面法线与场对应的量重合,这是可以做到的。("d"for diagonal,"c" for cross)
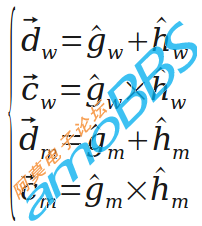
然后旋转分两步:首先使对角线重合,得到第一个旋转。
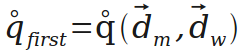
在第二次旋转前,要用第一个旋转变换一下测量量的平面法线。因为经过第一次旋转,测量量的平面法线也跟着转了。
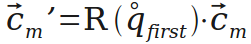
接着就是第二次旋转,使平面法线重合。
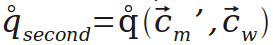
组合两次旋转,直接姿态就出来了。第一阶段完成。
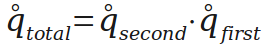
第二阶段是纠正当前姿态,这里用的是最简单的——线性插值再单位化。
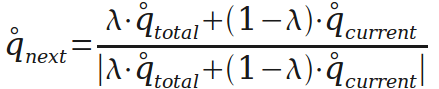 - 快速融合
快速融合比长期融合简单多了。
先用测得的角速度和积分间隔构造“微旋转”,这里用了小角三角近似,sin(Δ)≈Δ,cos(Δ)≈1。
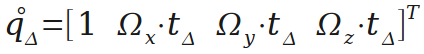
然后用四元数乘法组合,就成了。
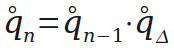
原文:http://blog.sina.com.cn/s/blog_81f1e26801016ub2.html
|